如何生成光滑曲线？

想象现在在平面上有一些已知坐标的点，有哪些方法可以把这些点用平滑曲线连接起来呢？

办法当然有很多，只要一google就会有一大堆插值算法，可惜每一个都看起来那么复杂，我都看不懂。除此之外，还有很多现成的库供你调用，但是如果我想要一个自己懂得原理的算法应该怎么办？

我花了很多时间来甄选用搜索引擎找的一大堆算法，终于找到一个原理简单，效果卓越的利用贝塞尔曲线的算法（bezier curves）。

原图

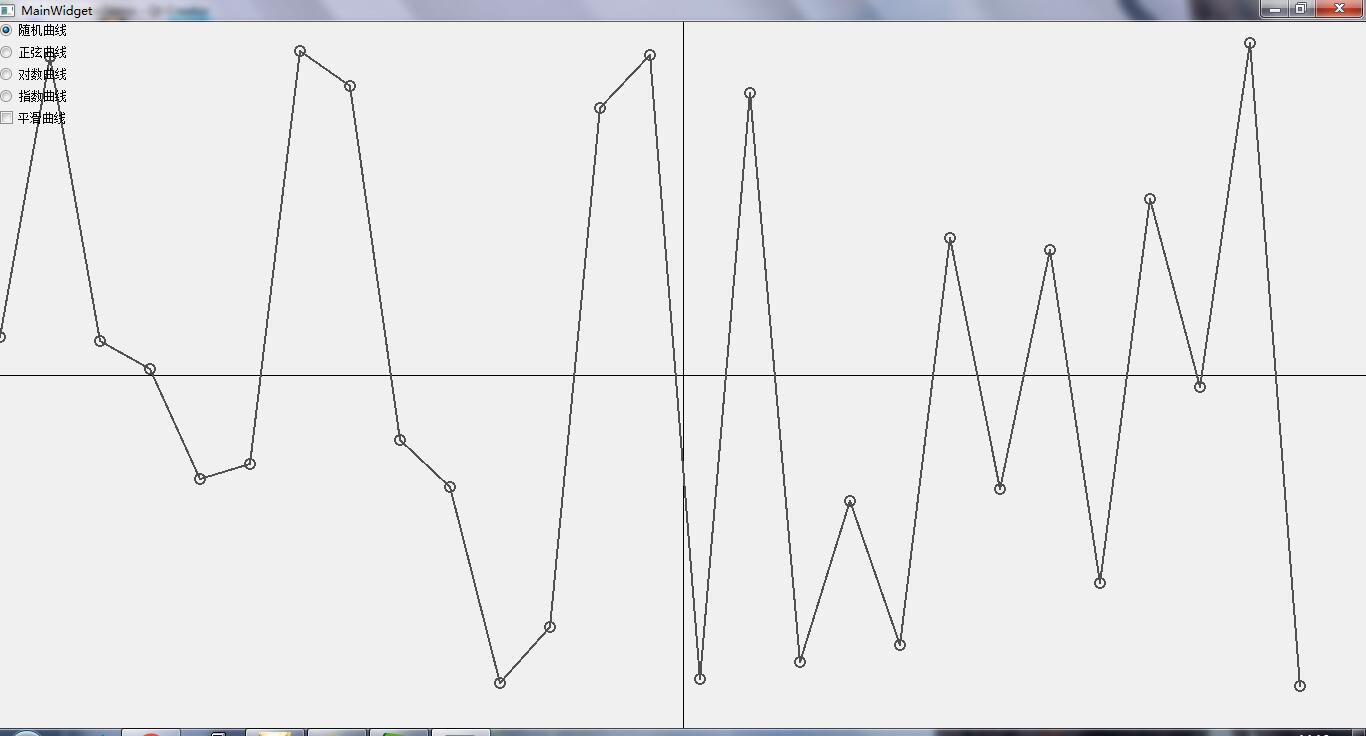
效果图

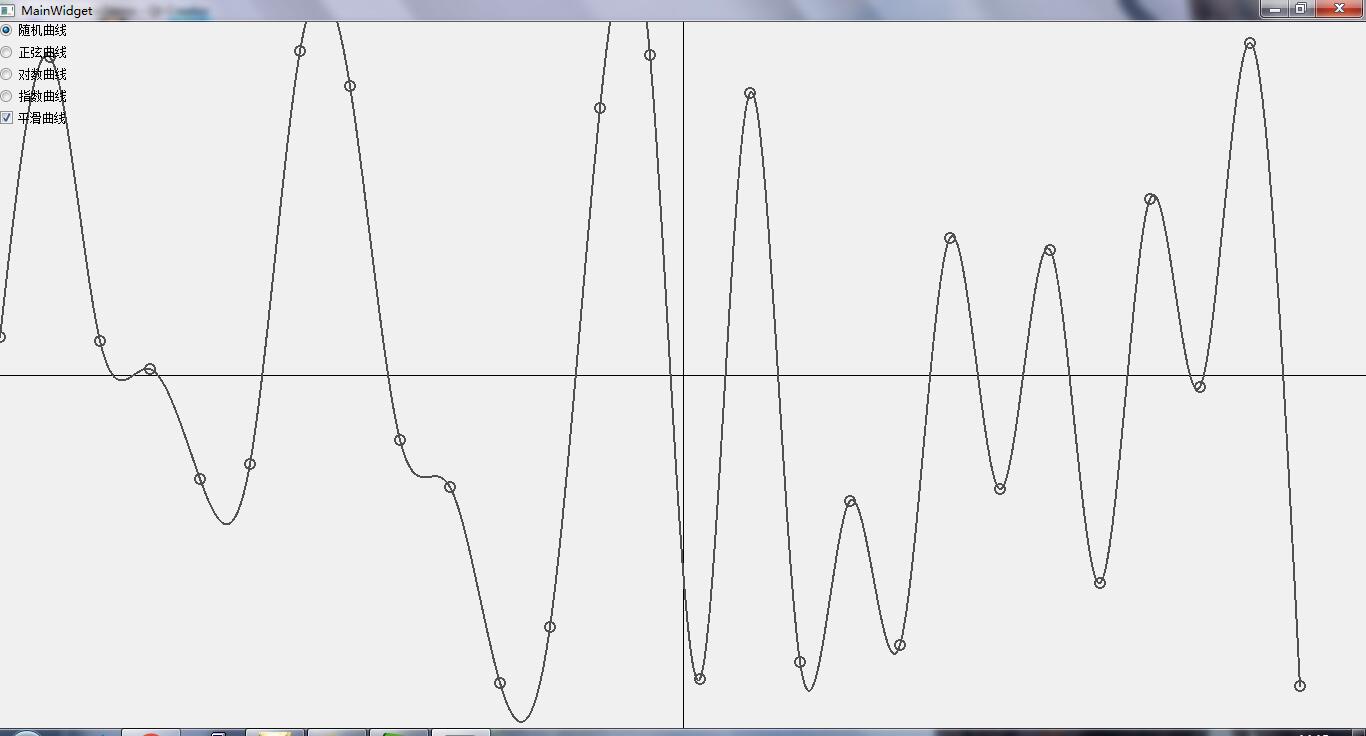
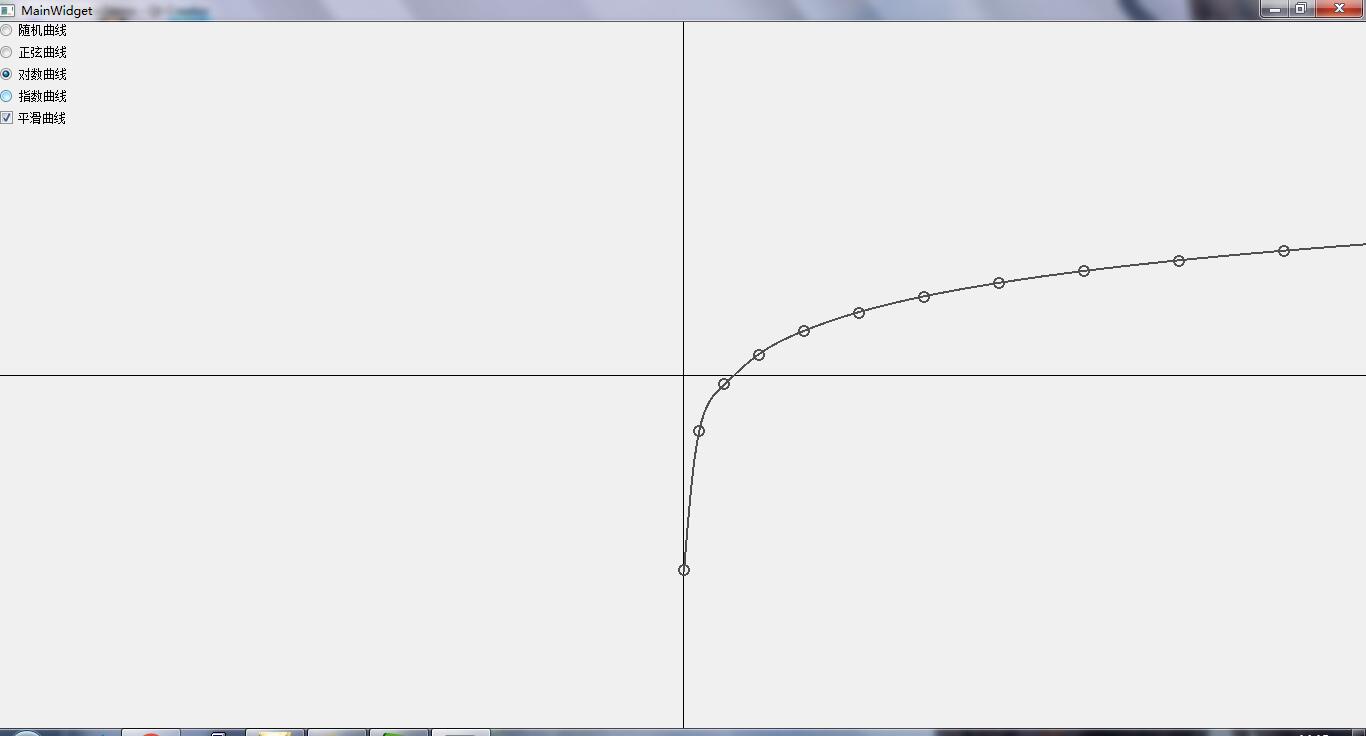
0x00 简单&高效？

之所以说这个算法简单是因为他推导的过程非常之简单且易懂，适用于任何高中及以上学历，安全无毒适宜人类和喵食用。

高效是因为这个算法不需要你详细计算出每个点，然后逐点描图，你要做的只是根据已知点的坐标然后计算出贝塞尔曲线的控制点，其他就只需要交给图形框架替你渲染了。（前提是你所使用的图形框架提供了绘制贝塞尔曲线的函数或者方法，当前流行的主流的图形框架都提供了这一方法，例如Qt Gui）

0x01 贝塞尔曲线?

可能有很多人并不了解贝塞尔曲线，但是你可能在哪听说过（我第一次听说这个名词是在windows XP的屏幕保护程序里面，在里面有一个就叫贝塞尔曲线(笑)），而事实上你也经常会使用到这个曲线或者这个曲线的成果。

贝塞尔曲线的数学基础是早在 1912 年就广为人知的伯恩斯坦多项式。但直到 1959 年，当时就职于雪铁龙的法国数学家 Paul de Casteljau 才开始对它进行图形化应用的尝试，并提出了一种数值稳定的 de Casteljau 算法。然而贝塞尔曲线的得名，却是由于 1962 年另一位就职于雷诺的法国工程师 Pierre Bézier 的广泛宣传。他使用这种只需要很少的控制点就能够生成复杂平滑曲线的方法，来辅助汽车车体的工业设计。

正是因为控制简便却具有极强的描述能力，贝塞尔曲线在工业设计领域迅速得到了广泛的应用。不仅如此，在计算机图形学领域，尤其是矢量图形学，贝塞尔曲线也占有重要的地位。今天我们最常见的一些矢量绘图软件，如 Flash、Illustrator、CorelDraw 等，无一例外都提供了绘制贝塞尔曲线的功能。甚至像 Photoshop 这样的位图编辑软件，也把贝塞尔曲线作为仅有的矢量绘制工具（钢笔工具）包含其中。

贝塞尔曲线在 web 开发领域同样占有一席之地。CSS3 新增了 transition-timing-function 属性，它的取值就可以设置为一个三次贝塞尔曲线方程。在此之前，也有不少 JavaScript 动画库使用贝塞尔曲线来实现美观逼真的缓动效果。 来源： 米粽粽

0x02 算法的推导

最常用的贝塞尔曲线具有两个控制点，也就是说要绘制P0到P1的贝塞尔曲线你还需要计算出这个点的控制点，其中起点和终点通常被叫做knot point，而控制点被称作control point。两个点之间的贝塞尔曲线表示为：

Tips：其中t为属于区间[0,1]的参数。P0和P3为起点和终点(knot point)，而P1和P2分别靠近P0和P3的控制点(control point)。你可能会感到疑惑，P为点怎么和实数进行运算，在这里我们规定：若P为点(X,Y),P1为点(M,N),那么P*t=(t*X,t*Y),P+P1=(X+M,Y+N).

那么如何自己逐点绘制这个曲线呢？

令t从0到1以步长为x递增，按照上述方法计算得到的B(t)都位于曲线上，连接这些点，就得到了曲线，其中x越小得到的曲线就越精确，你可以自己选定起点和终点还有控制点，然后把自己逐点绘制的曲线和gui框架提供的贝塞尔绘图函数得到的曲线对比一下，当然，gui框架绘制的曲线一般比自己绘制的好看且高效的多……

既然如此，那我们所需要做的工作就只是根据已知的n个点的坐标，计算出控制点，然后绘制就行了，只有3步，是不是很简单？

QAQ我们继续……

我们先规定格式好了，便于推导：

1.Pi-为第i个knot point，一共n+1个。

2.P1i-为靠近Pi的第一个控制点。

3.P2i-为靠近$Pi$的第二个控制点。

所以在第i段曲线，方程为：(i=1~n) 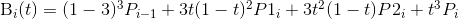对这个函数进行求导，结果为：

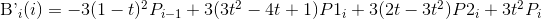
我们先反过来想一想，假如我们已经得到了连接各个点的光滑曲线，曲线由一段段的子贝塞尔曲线组合而成，那么显然有：前面一段贝塞尔曲线最后一个点导函数的值等于后一段贝塞尔曲线的第一个点的导函数值，即：

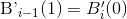
由此可得：(1)

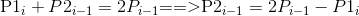
现在我们有了一个方程，然后我们对贝塞尔曲线再进行二阶求导:(i=1~n)

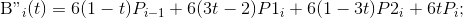
同理可知$B’’_{i-1}(1)=B’’_i(0)$ ，可得:(2)

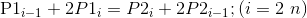
此外，我们假设第一个点和最后一个点处有B”1(0) = 0 and B”n(1) = 0.可得：(3):

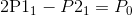
(4):

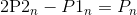
然后我们得到了2n个方程组和2n个未知数（即控制点），显然是可以通过简单的消元把控制点解出来，我们先联立方程(1)和方程(2)，消去所有P2点，得到如下方程组：

……

……

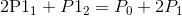
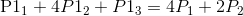
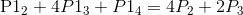
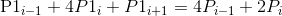
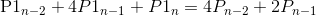
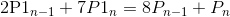
然后就简单了，这个方程组明显是环环相扣，可以很简单的进行消元，解出所有P1点，再利用方程(1)即可由P1得到P2点，至此所有控制点已经解出来了，由于两段曲线接点处斜率相同（一阶导函数值相同），且二阶导函数值相同，保证函数值平稳变化，所以由各段贝塞尔曲线组成的大曲线也是平滑的曲线。

下面给出了代码，是我自己写的一个demo，先生成一些点，然后利用此算法生成平滑曲线，大家可以看到效果是很显著的。我自己的demo是用 Qt 写的，版本是 Qt5.2 ，类SmoothCurveCreator即是用于生成平滑曲线的类，他的构造函数接受一个装有原始点(knot points)的QList，生成控制点和QPainterPath，可以用QPainter::drawPath，直接绘制出曲线，同时在demo里面通过生成点来拟出一些常见函数，准确度较高。

SmoothCurveCreator.h

#ifndef SMOOTHCURVECREATOR_H
#define SMOOTHCURVECREATOR_H
#include <QList>
#include <QPainter>

class SmoothCurveCreator
{
public:
    SmoothCurveCreator(QList<QPointF> knots);
    QList<QPointF> ctrlPoint1,ctrlPoint2;
    QPainterPath path;
};

#endif // SMOOTHCURVECREATOR_H

SmoothCurveCreator.cpp

#include "SmoothCurveCreator.h"

SmoothCurveCreator::SmoothCurveCreator(QList<QPointF> knots)//消元求解
{
    int n=knots.size()-1;
    QPointF rsp[n];
    for(int i=1;i<=n-2;i++)
    {
        rsp[i].setX(4*knots[i].x()+2*knots[i+1].x());
        rsp[i].setY(4*knots[i].y()+2*knots[i+1].y());
    }
    rsp[0].setX(knots[0].x()+2*knots[1].x());
    rsp[0].setY(knots[0].y()+2*knots[1].y());
    rsp[n-1].setX( ( 8*knots[n-1].x()+knots[n].x() )/2.0 );
    rsp[n-1].setY( ( 8*knots[n-1].y()+knots[n].y() )/2.0 );

    QPointF internal[n];
    QPointF temp[n];

    double b1=2.0,b2=2.0;
    internal[0].setX(rsp[0].x()/b1);
    internal[0].setY(rsp[0].y()/b2);
    for(int i=1;i<n;i++)
    {
        temp[i].setX(1/b1);
        temp[i].setY(1/b2);
        b1=(i<n-1?4.0:3.5)-temp[i].x();
        b2=(i<n-1?4.0:3.5)-temp[i].y();

        internal[i].setX((rsp[i].x()-internal[i-1].x())/b1);
        internal[i].setY((rsp[i].y()-internal[i-1].y())/b2);
    }
    for(int i=1;i<n;i++)
    {
        internal[n-i-1].setX(internal[n-i-1].x()-temp[n-i].x()*internal[n-i].x());
        internal[n-i-1].setY(internal[n-i-1].y()-temp[n-i].y()*internal[n-i].y());
    }
    ctrlPoint1.reserve(n);
    ctrlPoint2.reserve(n);
    for (int i=0;i<n;i++)
    {
        ctrlPoint1.append(internal[i]);
        if(i<n - 1)
           ctrlPoint2.append(QPointF(2*knots
                                          [i+1].x()-internal[i+1].x(),2*
                   knots[i+1].y()-internal[i+1].y()));
        else
           ctrlPoint2.append(QPointF((knots
                                           [n].x()+internal[n-1].x())/2,
                   (knots[n].y()+internal[n-1].y())/2));
    }
    this->path.moveTo(knots[0]);
    for(int i=0;i<n;i++)
    {
        this->path.cubicTo(ctrlPoint1[i],ctrlPoint2[i],knots[i+1]);
    }
}

Demo的Qt工程代码在这里下载：SmoothCurvePro